Write Fast Robotics Code: Transcendental Footguns
Introduction
There’s premature optimization, and there’s doing things right the first time.
Figure 1: There seems to be an xkcd comic for everything (link).
For roboticists, we have to split the time between thinking about the next great motion planning algorithm, and debugging C++ code without unit tests written by sleep deprived graduate students. As a result, saving developer time by doing things right on the first try is especially important.
If you have read any robotics paper, you will know that we love trigonometry. A lot of times this is out of necessity: robots operate in 3D, and we use the basic Euclidean geometry tools to describe it.

Figure 2: A fragment of the second book of the Elements of Euclid containing the 5th proposition. Translation by T. L. Heath: If a straight line be cut into equal and unequal segments, the rectangle contained by the unequal segments of the whole together with the square on the straight line between the points of section is equal to the square on the half. (link for more explanation)
However, when translating these algorithms involving trigonometric functions (or more generally, transcendental functions) into programs, a common mistake is to do it verbatim without considering the underlying computation costs and accuracy.
In this post, I will show the potential benefits if we avoid transcendental functions, and provide a few tips on how to do so. I will also discuss the decisions we have to make if we want to use transcendental functions effectively, and provide some suggestions on libraries to use.
What are transcendental functions?
Informally, transcendental functions are functions that cannot be expressed by polynomial equations. In other words, you cannot express a transcendental function with a finite number of basic algebraic operations such as additions, multiplications, divisions and subtractions.
Common examples of transcendental functions include:
\begin{align} f_{1}(x) = \sin(x) \\ f_{2}(x) = x^{1/x} \\ f_{3}(x) = \log(x) \end{align}
In popular library implementations, depending on the accuracy requirements the actual code used may switch between different algorithms depending on the inputs.
For example, in glibc’s s_sin.c, the sine function looks like this:
/*******************************************************************/ /* An ultimate sin routine. Given an IEEE double machine number x */ /* it computes the rounded value of sin(x). */ /*******************************************************************/ #ifndef IN_SINCOS double SECTION __sin (double x) { double t, a, da; mynumber u; int4 k, m, n; double retval = 0; SET_RESTORE_ROUND_53BIT (FE_TONEAREST); u.x = x; m = u.i[HIGH_HALF]; k = 0x7fffffff & m; /* no sign */ if (k < 0x3e500000) /* if x->0 =>sin(x)=x */ { math_check_force_underflow (x); retval = x; } /*--------------------------- 2^-26<|x|< 0.855469---------------------- */ else if (k < 0x3feb6000) { /* Max ULP is 0.548. */ retval = do_sin (x, 0); } /* else if (k < 0x3feb6000) */ /*----------------------- 0.855469 <|x|<2.426265 ----------------------*/ else if (k < 0x400368fd) { t = hp0 - fabs (x); /* Max ULP is 0.51. */ retval = copysign (do_cos (t, hp1), x); } /* else if (k < 0x400368fd) */ /*-------------------------- 2.426265<|x|< 105414350 ----------------------*/ else if (k < 0x419921FB) { n = reduce_sincos (x, &a, &da); retval = do_sincos (a, da, n); } /* else if (k < 0x419921FB ) */ /* --------------------105414350 <|x| <2^1024------------------------------*/ else if (k < 0x7ff00000) { n = __branred (x, &a, &da); retval = do_sincos (a, da, n); } /*--------------------- |x| > 2^1024 ----------------------------------*/ else { if (k == 0x7ff00000 && u.i[LOW_HALF] == 0) __set_errno (EDOM); retval = x / x; } return retval; }
__sin(x) uses different algorithms for different ranges of x.
To better understand this, first note that mynumer is a union type:
typedef union { int4 i[2]; double x; double d; } mynumber;
int4 is a 4-byte integer type, and double is a 8-byte float type.
The code then does more bit twiddling on x:
u.x = x; m = u.i[HIGH_HALF]; k = 0x7fffffff & m; /* no sign */
The statement m = u.i[HIGH_HALF] is essentially accessing the leading 4-byte of x.
And k = 0x7fffffff & m removes the sign of m (0x7fffffff in binary is all ones except a zero at the front).
Therefore, at this stage k represents the sign (1 bit), exponent (11 bits) and leading digits (20 bits) of mantissa of x.
If x is small, it directly returns x:
if (k < 0x3e500000) /* if x->0 =>sin(x)=x */ { math_check_force_underflow (x); retval = x; }
To see that, note that 0x3e5 is 997 in decimal,
which represents an exponent of -26 (in IEEE floating point number representations, the exponent is biased and we need to subtract 1023 from it).
Hence, k < 0x3e500000 is equivalent to checking whether x is less than 2e-26.
Similarly, for the other branches it also checks the range in which x falls into.
And depending on the range, it may use either do_sin, which involves a lookup table, or first reduce the value into within \(\pi/2\),
and use do_sin again.
Similarly, the implementation for the power function (__pow(double x, double y)) also involves choosing algorithms based on input values, and a lot of bit twiddling tricks.
It is a bit more convoluted than __sin(double x), so I won’t go into details here.
Nevertheless,
the key idea remain the same: evaluating transcendental functions is difficult.
Transcendental functions are slow
The inherent complexity of transcendental functions can manifest itself in two ways: speed and accuracy. I will focus on showing the former through numerical experiments. For the latter, please take a look at this excellent blog post by Bruce Dawson: Intel Underestimates Error Bounds by 1.3 quintillion
You can find the following code samples here.
First, let’s take a look at the difference between acos and a dot product.
Here are the two benchmark functions:
// benchmark function for acos double bench_acos(std::vector <std::tuple<double, double>> &a, std::vector <std::tuple<double, double>> &b) { double result = 0; for (size_t i = 0; i < ITERATIONS; ++i) { for (size_t j = 0; j < a.size(); ++j) { result += std::acos(std::get<0>(a[j]) * std::get<0>(b[j]) + std::get<1>(a[j]) * std::get<1>(b[j])); } } return result; } // benchmark function for dot products double bench_dot(std::vector <std::tuple<double, double>> &a, std::vector <std::tuple<double, double>> &b) { double result = 0; for (size_t i = 0; i < ITERATIONS; ++i) { for (size_t j = 0; j < a.size(); ++j) { result += std::get<0>(a[j]) * std::get<0>(b[j]) + std::get<1>(a[j]) * std::get<1>(b[j]); } } return result; }
The two benchmark functions essentially just compute arccosine and dot products.
It should be pretty obvious that the arccosine version does more work than that of the dot product.
But by exactly how much? Here are the timing results if I run them on my desktop with perf stat:
| dot | acos | |
| float | 46.27 msec | 340.80 msec |
| double | 50.34 msec | 466.91 msec |
The columns are the two different benchmarks with arccosine vs. dot products, and the two rows are with the different floating number types (float vs. double). In the case for doubles, the arccosine version is 9 times slower. Note that the generation of the random numbers only take around 3 milliseconds, so the bulk of the differences lie within the difference between dot products and arccosine functions. One potential culprit is the total number of ranch misses. For the arccosine version, there are around 2 million branch misses, whereas for the dot product version, there are only around 100 thousands branch misses.
Now, let’s take a look at the pow function.
Here are the benchmarks:
// use std::pow double bench_std_pow(int exp) { double result = 0; for(size_t i = 0; i < ITERATIONS; ++i){ result += std::pow(static_cast<double>(i), exp); } return result; } // just multiply double bench_pow_4() { double result = 0; for(size_t i = 0; i < ITERATIONS; ++i){ double base = static_cast<double>(i); result += base * base * base * base; } return result; }
Essentially, we are comparing the pow function from the standard library to simple multiplications (3 multiplications).
The following table shows the timing results (10 million iterations):
| float | double | |
| mul | 12.48 msec | 15.92 msec |
| pow | 125.67 msec | 118.00 msec |
In the case of doubles, we have about a 7 times slow down going from multiplications to pow.
In the case of floats, the slow down ratio is about 10:1.
For a more dramatic case of pow being excruciatingly slow,
take a look at Jason Summers’ article Slow power computation by 64-bit glibc (about 8000 times slower with some inputs!).
Tips on optimizing transcendental functions in robotics code
At this stage, it should be clear that transcendental functions are slow. While possible, we should always aim to reduce the use of them in our code, especially those running on real robots. While it is impossible to provide a mechanical way to replace transcendental functions in all algorithms, based on my experience I have a few actionable tips that should work well in general.
Measure twice, optimize once
It may seem contrary to what I have just said, but don’t start hastily optimizing away transcendental functions before measuring its performance. If it’s already fast enough for your application, then spend your energy somewhere else!
Start with the derivation
Depending on the problem you are solving, a lot of times you can avoid explicitly calling transcendental functions all together. Take a look at Laurent Kneip’s paper on his P3P solver. By keeping all the trigonometric functions intact and use lots of trigonometric identities, he avoided all transcendental functions and only requires solving a quartic equation which has a closed-form solution.
Use integers if possible
As we’ve seen earlier, just calculating the dot product is about an order of magnitude faster than calculating the floating point power. In terms of exponentiation, there exists specialized algorithm that works on integers (see exponentiation by squaring).
What if you have to use transcendental functions?
Despite your best efforts, there are still various places where you have to use transcendental functions. In these cases, choosing the right algorithm and implementation based on your requirements is crucial. In fact, it might be the easiest optimization you can do to greatly improve your code’s performance.
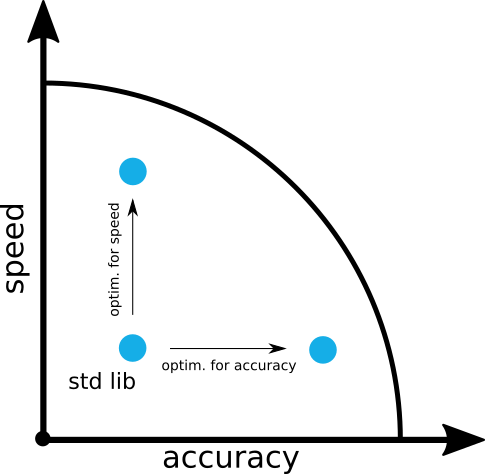
Figure 3: Optimizing transcendental function performance needs to decided between speed and accuracy.
On a very high level, different algorithms make different tradeoffs between speed and accuracy. Every time a transcendental function is evaluated, the computer is calculating an approximation. And as an approximation, you can trade accuracy with speed (or vice versa). Hence, if you make informed decisions on the algorithms to use based on your requirements, you have already made huge strides in achieving the optimal performance you can get — moving towards the boundary of the trade off curve (Fig. 3) in the direction you want.
Nevertheless, if you have to implement the specific algorithm yourself, it will still be a painful experience. Luckily, we have access to various excellent numerical libraries. One of those is GNU Scientific Library (GSL), which implements many routines for transcendental functions that give you both the results and an error estimate.
For example, if you need to calculate the integer power, they have a dedicated routine for it called gsl_pow_int(double x, int n).
And if you need to calculate \(\log{(1+x)}\) while knowing that \(x\) is small, then you can use a routine called gsl_log1p(const double x).
The library is implemented in C and everything is thread-safe.
If you don’t need to use C/C++, take a look at Julia. Julia offers an extensive selection of mathematical functions, and with its extensive numerical package ecosystem you should be able to bootstrap your project in no time.